첫 번째 풀이 코드
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 | import sys from heapq import heappush, heappop n, m, x = map(int, input().split()) data = [[] for _ in range(n + 1)] INF = int(1e9) for _ in range(m): a, b, c = map(int, sys.stdin.readline().split()) data[a].append((b, c)) def dijkstra(start, end): distance = [INF for _ in range(n+1)] distance[start] = 0 q = [] heappush(q, (0, start)) while q: dis, node = heappop(q) if distance[node] < dis: continue for i in data[node]: cost = dis + i[1] if distance[i[0]] > cost: heappush(q, (cost, i[0])) distance[i[0]] = cost return distance[end] def solved(): result = [0 for _ in range(n+1)] for i in range(1, n+1): start = dijkstra(i, x) end = dijkstra(x, i) result[i] = start+end print(max(result)) solved() | cs |
참고 블로그 풀이 코드
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 | import sys from heapq import heappush, heappop input = sys.stdin.readline n, m, x = map(int, input().split()) inf = 100000000 s = [[] for i in range(n + 1)] dp = [inf] * (n + 1) s_r = [[] for i in range(n + 1)] dp_r = [inf] * (n + 1) def dijkstra(start, dp, s): heap = [] dp[start] = 0 heappush(heap, [0, start]) while heap: w, n = heappop(heap) if dp[n] < w: continue for n_n, wei in s[n]: n_w = wei + w if n_w < dp[n_n]: dp[n_n] = n_w heappush(heap, [n_w, n_n]) for i in range(m): a, b, t = map(int, input().split()) s[a].append([b, t]) s_r[b].append([a, t]) dijkstra(x, dp, s) dijkstra(x, dp_r, s_r) max_ = 0 for i in range(1, n + 1): max_ = max(max_, dp[i] + dp_r[i]) print(max_) | cs |
참고: pacific-ocean.tistory.com/282
두 코드의 시간 복잡도 차이

첫 번째 코드 풀이 해석
dijkstra함수는 매개변수 start를 노드의 출발점으로 지정한 후, start부터 모든 노드까지의 최단 거리를 구하였다.
그 후, 도착지점 end까지의 최단거리를 반환하였다.
solved()안에 for문의 의미는, dijkstra함수를 호출하여 각 노드 시작점-X(도착지점)까지의 최단 거리를 구한 후
또 한번 dijkstra 함수를 호출하는데, 이번에는 반대로 하여 시작점부터 도착점과 도착점부터 시작점까지의 두개 거리를 더하여 저장하였다.
두 번째 코드 풀이 해석
첫 번째 코드 풀이와 동일하지만, 다른점은 그래프를 저장할 때 두개의 리스트로 저장하는 것이다.
단방향 그래프 하나만을 저장하는 것이 아니라,
s[a].append([b, t])
s_r[b].append([a, t])
이 부분을 통하여 단방향 그래프 두개를 저장한 것이다.
그 후, 두번의 dikstra함수를 호출하여 dp, dp_r 리스트 각각에 x에서 출발하여 모든 노드까지의 최단거리를
가는 경우와 오는 경우 두가지를 모두 저장하였다.
for i in range(1, n + 1):
max_ = max(max_, dp[i] + dp_r[i])
그리고 해당 코드를 통해 가장 긴 거리를 계산하였다.
Why?
이전 회고를 통해, 앞으로의 문제 리뷰에는 "왜?"라는 질문을 계속 던지기로 했다.
Q1. dp, dp_r은 어떻게 갈 경우와 올 경우의 최단거리를 저장할 수 있게 된건가?
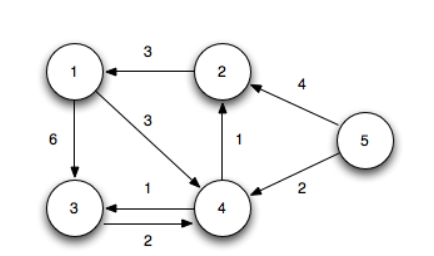
그림과 같은 그래프가 있다고 가정했을 때, 그림과 같은 화살표로 dijkstra를 구한 후
현재 화살표를 반대로만 다 바꾸고 dijstra를 구한다면
갈 때와 올 때의 모든 노드 최단 거리를 구할 수 있다.
+ 이런건 직접 그려보는게 가장 이해가 빠른 것 같다. 직접 그려보자.
Q2. 나는 왜 저런 방식을 떠올리지 못했을까?
이 질문을 스스로에게 하다 보니 이상한 점을 발견했다.
end = dijkstra(x, i)
나는 이 코드를 돌아가는 거리를 구하는 것으로 사용했는데, 이게 어떻게 돌아가는 거리를 구해준 걸까?
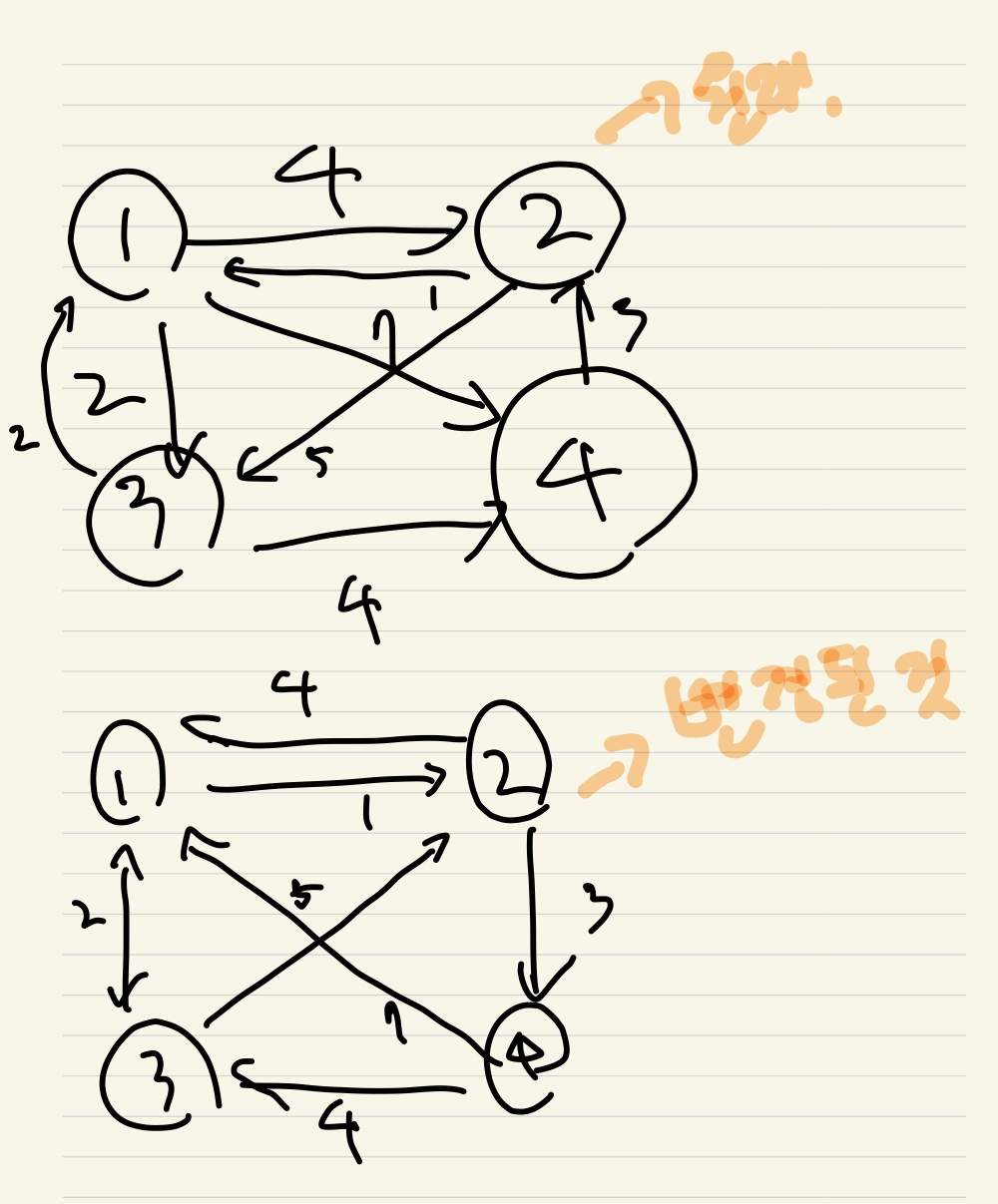
직접 그려보니, dp가 돌아가는 최단 거리를 저장하는 리스트이고
dp_r이 각 지점에서 목적지까지 가는 최단 거리를 저장하는 리스트였다.
왜 이게 가능한걸까..??😮
왜 이게 돌아가는 거리이고, 지나가는 거리를 구한 것이 된거지..?
답: 2에서 도착한 후, 돌아가는 상황을 생각해보면
출발점을 2로 하여 dijkstra를 수행하면 돌아가는 경우가 나오게 된다.
또 방향선을 전부 반대로 바꾼 후, 출발점을 2로 한다면
각 지점에서 2까지의 최단 거리를 계산해 준 것이 나온다.
-> 정답을 본 이후여도 이해하는데 시간이 오래걸렸다.
나혼자 생각했다면, 생각하기 어려웠을 것이다.
그냥 바로 넘어가지 말고 좀 더 이해할 만한 것이 있나 곰곰히 생각해보자.
'개발 > 알고리즘' 카테고리의 다른 글
| [백준 / Python] 줄 세우기_2252 (0) | 2021.04.29 |
|---|---|
| [백준 / Python] 네트워크 연결_1922 (0) | 2021.04.28 |
| [BOJ] 좋은수열_2661 (0) | 2021.04.08 |
| [BOJ] 차이를 최대로_10819 (0) | 2021.04.06 |
| [BOJ] 행성 터널_2887 (0) | 2021.04.03 |



